3D Metaballs

The metaballs effect was created by Jim Blinn for Carl Sagan's show Cosmos. The core concept is simple, but the implementation has a lot of moving parts.

Controls

Desktop
Click to enter interactive mode
Esc to exit interactive mode
Move mouse: rotate camera
W/S: move camera forward/backward
A/D: move camera left/right
E/Q: move camera up/down
Hold shift: move camera faster
Space: pause/play

How it Works

There are four major elements to this demo: isosurfaces, marching cubes, GPU computation, and WebGL compute shaders.

Isosurfaces

At a high level, metaballs are based on one thing: a grid of numbers. This grid exists throughout space, and the metaballs simply exist where the numbers are big enough. In other words, metaballs are clumps of big numbers in this grid.

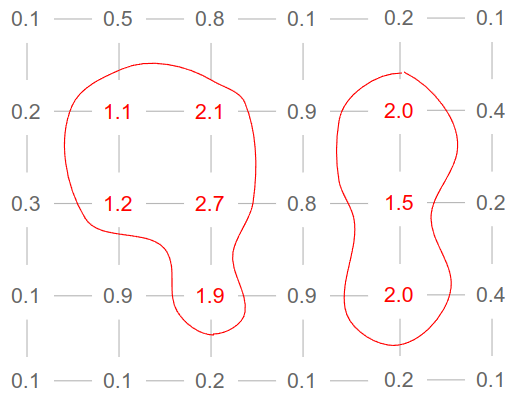
A grid like this is called a scalar field, since in the math business, we often call numbers scalars. If you pause the demo and fly up to the smaller spheres, you might notice some faint edges. These are the grid lines that make up the metaballs.

---

But how do we actually go from a grid to a smooth metaball surface? We do so by splitting the grid into regions based on the numbers. An astute reader may notice that all of the numbers inside the red regions are greater than one, and all of the other numbers are less than one. The surface dividing these two regions is called an isosurface, and that's what we end up drawing. The name comes from the Greek "isos", meaning "equal", and because it splits the regions greater than one and less than one, we think of the surface as being equal to one everywhere, hence an "equal surface".

Marching Cubes

We know that we need to construct an isosurface, but the way we do that isn't totally clear. Luckily an algorithm exists to do exactly that, called marching cubes. The algorithm is a bit too complicated to go into detail here, but for anyone interested, Sebastian Lague has a fantastic explanation in video form. The upshot is that it allows us to create something like this:

The fineness of the grid has been reduced for clarity, but save for the lack of color, this looks pretty similar to the demo shown here. However, there's one major problem that hasn't been addressed yet.

GPU Computation

Computers are only so powerful. Our processor can perform billions of operations every second, but even it has its limits. Graphics cards, surprising as it may be, are actually many, many times more powerful than most processors if used correctly. For the task of determining the shape of our metaballs, we can efficiently wield our graphics card.

We can think of a computer's processor as one really smart person doing calculation after calculation. This works perfectly for most tasks, but it fails at parallelism. If we have many tasks we want to do at the same time, they must wait their turn to be completed, as the computer can only do one thing at a time. Graphics cards are the opposite: instead of one really smart person, the graphics card is more like 1,000 fifth graders. Not particularly capable on their own, sure, but with some organization, they can easily outmatch one person.

This is where the metaballs come in: we need to calculate a number at each point in the grid. The calculation for each grid point is the same, so we can tell each fifth-grader in our graphics card to do the math for a few grid cells, and together, they come up with a result way faster than our processor could have.

WebGL Compute Shaders

The most common way to interface with graphics cards on the web is with WebGL. Unfortunately, WebGL only lets us send very specific instructions to the GPU, and if this set of instructions doesn't offer what we need, we're out of luck.

We would like to tell the graphics card to run the metaball calculations. Normally, we would do this using something called a compute shader, but WebGL doesn't let us use these. Instead, we need to be clever about it. In this case, the solution is to tell WebGL to draw a picture, where the brightness of each pixel in the picture is the result of our metaball computation. Some may call it inelegant, but this allows us to utilize our GPU to its fullest potential.