Complex Numbers are Secretly Polynomials

September 2, 2023

8 and 14 are equal, mod 3. They have the same remainder, so this should come as no surprise. Let's draw it out anyway.

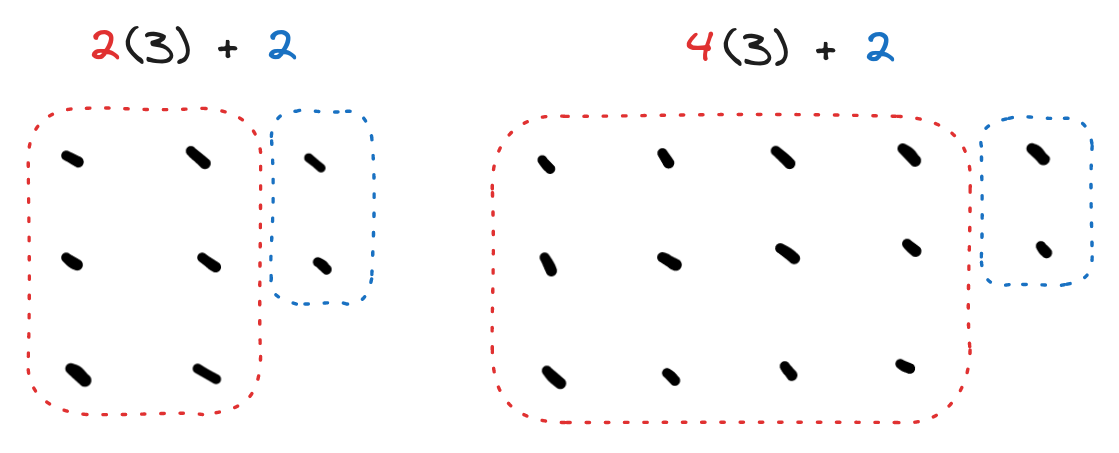
To observe the painstakingly obvious: each collection of dots can be split into the form $Q$$(3) +$$R$, where $Q$ is the quotient and $R$ is the remainder. If you ignore the $Q$ part, you see that 8 and 14 have the same value of $R$, $2$, so they're the same, mod 3. We call two numbers equal under this system if they differ only by a multiple of 3.

What does this have to do with complex numbers or polynomials? All in due time.

The Naive Approach

If I were to ask you to give me a polynomial representation of a complex number, you'd probably give me something like

It's the first thing any reasonable person would come up with, and for good reason: $\varphi(0) = 0$, $\varphi(1) = 1$, and addition works the same in both spaces. But there's a glaring issue -- multiplication doesn't work. If we multiply out two of our polynomials, we get

which doesn't fit into our paradigm (note the $x^2$). Our problem here is that polynomials don't capture the essence of complex numbers -- nothing in $a + bx$ screams $i^2 = -1$, because $x$ is too generic a standin for $i$. Let's look at another example where polynomial multiplication goes wrong. Consider:

We get different answers, but different how? I've written it a bit suggestively, but you might notice that the difference between the two results is $x^2 + 1$, the defining polynomial for $i$. Coincidence? Let's try another.

So we should get an answer of $292 + 256i$. This doesn't happen automatically in the polynomial case, but if we factor out the $x^2 + 1$ term, we get

It looks like we get the answer we expect on the right but with this extra term on the left. At this point, it might become clear what's happening: if we substitute $i$ for $x$ like discussed earlier, the $x^2 + 1$ vanishes and we get the answer we want. Every polynomial can be split into an $x^2 + 1$ part and a remainder part, $Q$$(x^2 + 1)\ +\$$R$ (in our case, $Q$ $= -24x - 82$ and $R$ $= 292 + 256x$), so we just ignore the $Q$ part. But that's not the end of the story -- to really understand what's going on, we need to talk about quotient sets.

Quotient Sets

As we saw earlier, $\mathbb R[x]$ already almost behaves like $\mathbb C$, and it works perfectly if you treat $x^2 + 1$ like $0$. So all we need to do is split the polynomial into $Q$ and $R$ and just consider the $R$. How can we make this more precise?

This is where quotient sets come in. The expression $\mathbb R[x] / (x^2 + 1)$ (read "R[x] mod x-squared-plus-one".) tells us to work within $\mathbb R[x]$, but to "ignore" the $Q$ part -- if that sounds familiar, it's exactly what we did with division by 3 at the start of the article.^[1] Specifically, it calls two polynomials the same if they differ only by a multiple of $x^2 + 1$. This lines up with our understanding of complex numbers: if $z$ and $w$ differ by a multiple of $i^2 + 1$, are they really different?

Just like we can talk about integers mod 3, we can talk about polynomials mod $x^2 + 1$. In the integers mod 3, we explicitly say that $3 = 0$ and see what follows. In our quotient set, we explicitly say that $x^2 + 1 = 0$ and see what follows. In both cases, the statement "mod 3" or "mod $x^2 + 1$" is just a reminder that we're ignoring some part of the expression by forcing it to be zero.

Under this mapping, for example, the following polynomials would be equal

Since they all have the same remainder, mod $x^2 + 1$. Equivalently, if you plug in $x = i$, you'll see that they all evaluate to the same thing. Technically, we'd say $\mathbb C$ and $\mathbb R[x] / (x^2 + 1)$ are isomorphic, meaning they "act the same" with regards to addition and multiplication.^[2]

General Quotients

The fundamental idea here is that if we have a set of objects $S$, we can make a smaller version by considering some objects the same; in the case of $\mathbb R[x] / (x^2 + 1)$, $S$ is the set of polynomials, and we consider two the same if they differ by a multiple of $x^2 + 1$.

We can go much further than "two objects are the same based on their difference". In fact, we can construct a quotient set from just about any relation you want. If you have a set $S$ and a relation between objects $\sim$, you can begin reasoning about $S/\!\sim$.

1. Consider $\mathbb Z \times \mathbb Z$, the set of all pairs of integers. If we apply the relation $(a, b) \sim (c, d) \Longleftrightarrow ad = bc$, then congratulations! You've constructed $(\mathbb Z \times \mathbb Z) / \! \sim$, the set of fractions, also known as $\mathbb Q$.^[4] If it's unclear why, observe how you can cross-multiply two equal fractions and look at the formula you get.
2. The integers mod 5, written $\mathbb Z_5$, can be constructed using the relation $a \sim b \Longleftrightarrow 5\ \mathrm{divides}\ (a - b)$. Then, $\mathbb Z_5$ is nothing but $\mathbb Z / \! \sim$. Think about why we can only have 5 elements in this set!
3. Consider $\mathbb R^{3 \times 3}$ (the set of 3x3 matrices) and the relation $A \sim B \Longleftrightarrow \det A = \det B$. Because we consider two matrices the same if they have the same determinant, each collection of "equivalent" matrices can be identified by its determinant. So, $\mathbb R^{3 \times 3} / \! \sim$ behaves like $\mathbb R$ under multiplication, since determinants multiply when multiplying matrices.

Hopefully these examples have elucidated the convenience of quotient sets in mathematics. They're not always strictly necessary (you knew what a fraction was before reading this article), but they can allow us to construct complicated behavior by "filtering down" large, easy-to-describe objects.

1. In the language of ring theory, $\mathbb R[x]$ is actually read "R adjoin x", so the whole thing should be read "R-adjoin-x mod x-squared-plus-one". ↩
2. The term "isomorphic" comes from the Greek "iso-" meaning equal and "morphe" meaning shape, so understandably, we generally call two mathematical structures isomorphic if they have the same shape, i.e. behave the same. Specifically, this isomorphism would be a ring isomorphism. ↩
3. This should actually be called an equivalence relation. In general, a relation can really be anything we want, but equivalence relations have to follow three rules:
   • Reflexivity - For all $x$, $x \sim x$
   • Symmetry - $x \sim y$ implies $y \sim x$
   • Transitivity - $x \sim y$ and $y \sim z$ implies $x \sim z$
   These rules are all pretty intuitive, so I felt that their omission was warranted :) ↩
4. We also stipulate that $b, d \neq 0$, obviously. ↩