How to Count

November 19, 2023

In the map of mathematics, combinatorics (the study of counting) is a continent. Counting is fundamental to everything we do, so it's not a shock that it would occupy such a prominent spot in the collective consciousness of mathematicians.

You might think counting is easy; indeed, we learn to count from a young age. But counting the number of possible configurations of a Rubik's Cube, for example, is anything but easy. In such a scenario, the combinatorist's primary tool is symmetry.

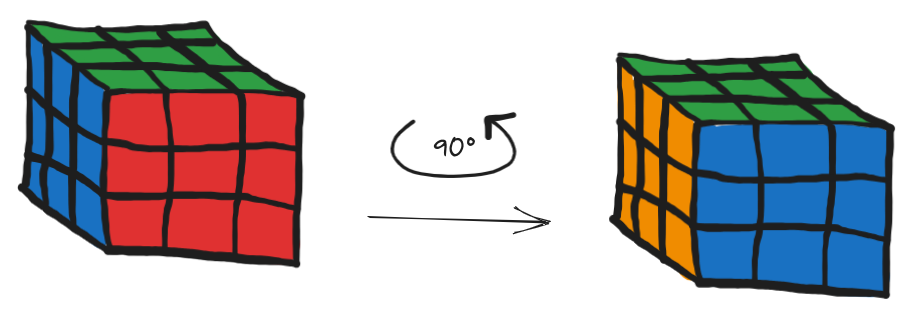
Consider how multiple different configurations of a Rubik's Cube are the same when you spin the cube around -- how we handle these symmetric arrangements has everything to do with counting problems.

Groups and Symmetry

You do not need to know anything about groups to understand this article. Everything you need to know is in this box.

It's always helpful to give names, so let's call the rotations of a cube $R$, and let $r$ be a 90° rotation, so $r \in R$ (the $\in$ symbol means "is contained in"). Then, we use the $\times$ to apply the rotation $r$ to the cube.

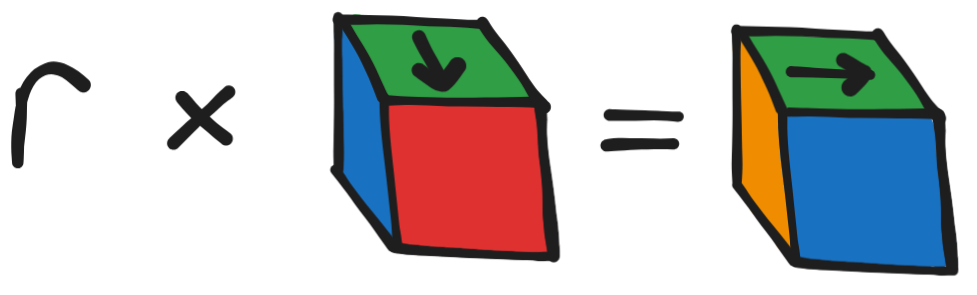
Importantly, observe that $r$ takes us from one coloring of the cube to a different coloring (we care about orientation, so red in front vs. blue in front matters). We need to make the distinction between rotations of the cube and the cube colorings themselves; continuing to name things, we'll call $X$ the set of cube colorings, and $R$ the set of rotations as before. Convince yourself that, if we have $n$ colors, there are $n^6$ colorings in $X$.^[1]

In the above diagram, we have two colorings $a$ and $b$, related by the equation $r \times a = b$. In particular, we have

1. $r \in R$ and $a, b \in X$.
2. $\times$ eats an $R$ and an $X$, and spits out an $X$, in the form $R \times X = X$.

Obviously, if you have a cube that's all red, rotating it around isn't gonna change the coloring. But it gets more complicated: for example, a cube that's green on the top and bottom, and yellow on the sides. Rotating up or down changes the coloring, but left and right doesn't.

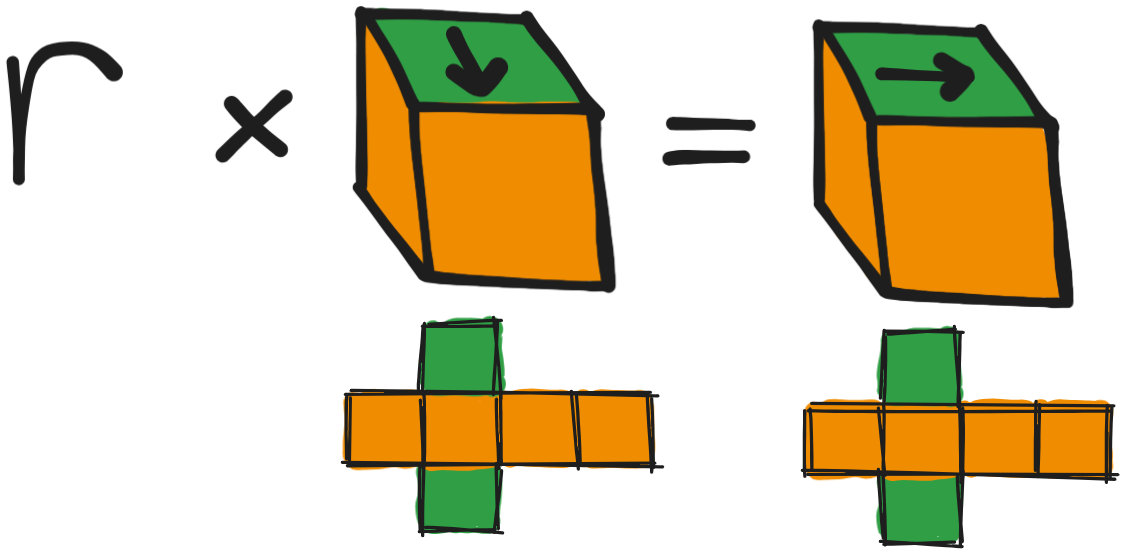
Algebraically, we'd write this as $r \times x = x$, and we'd say that $r$ fixes $x$, or that $x$ is a fixed point of $r$.

Orbits and Stabilizers

Let's flesh out this idea of fixed points. If we call the green-and-yellow cube from before $x$, it might be helpful to think about which rotations fix $x$. Counting them, there are 8 total (identity, spinning around, flipping). We call this collection of "fixing" rotations the stabilizer of $x$, or $R_x$, or just $\mathrm{Stab}(x)$ (I'm partial to the latter for readability).

What about everything else not in the stabilizer? Well, there are two other colorings that we could rotate $x$ to; we call this collection of "neighbor" colorings the orbit of $x$, or $G \times x$, or just $\mathrm{Orb}(x)$ (I'm partial to the latter, orb is a cool word). In this case, the orbit of $x$ has three elements:

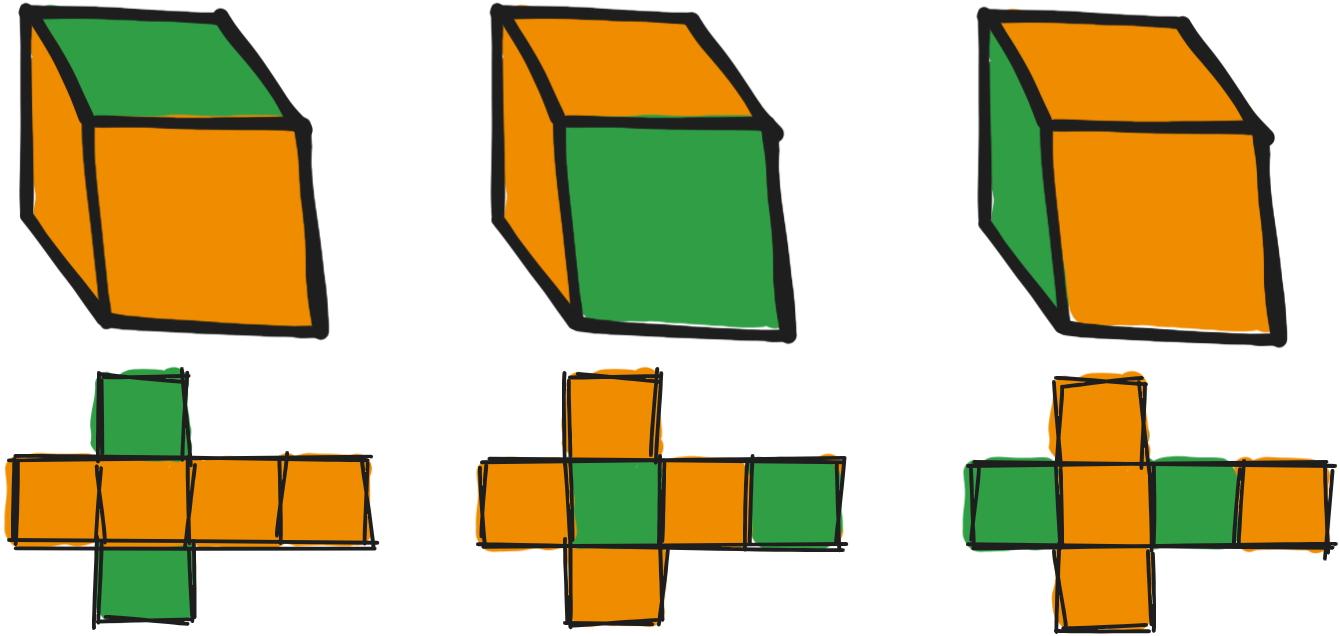
In general, orbit and stabilizer are inversely proportional; when stabilizer is big, orbit is small, and when stabilizer is small, orbit is big. Let's work through a couple examples.

1. Consider a cube that's all red. Every rotation gives you the same coloring, so the stabilizer is all of $R$. However, we're not able to get to any other colorings, so the orbit is just the cube itself.

2. Consider a cube that's different colors on all six sides. Every rotation changes the coloring, so the stabilizer is just the identity rotation. For the same reason, the orbit has one coloring for each rotation, so it's much larger.

The orbit-stabilizer theorem tells us that orbit and stabilizer vary inversely to each other.^[2] This should be intuitive: if lots of rotations fix your coloring, then they can't bring you to many new ones. Inversely, if your rotations generally don't keep you at the same coloring, they must bring you to lots of new ones.

Burnside's Lemma

This is the crown jewel. The usual formula looks like a bunch of notation, so I'll write it out in English:

In other words,

There's a lot going on here, but the underlying reasoning is pretty simple. If the size of stabilizers is large, then the size of orbits must be small (by the orbit-stabilizer theorem). If the orbits are small, there must be many of them, since each coloring is in some orbit. So large stabilizers equals many orbits.^[3]

The upshot is that we can use this formula to count orbits while only thinking about stabilizers. For example, say I want to count the number of colorings of the cube up to rotation, which if you think about it, is just asking how many orbits there are. This is normally a hard problem, but Burnside's Lemma lets us do it by counting fixed points, which is way easier.

1. For each face we have $n$ colors to choose from, i.e. there are $n$ ways to do it. Since there are six faces, there are $n \times \cdots \times n = n^6$ ways color the cube. ↩
2. It actually makes a stronger statement. For any $x \in X$, we have $|\mathrm{Orb}(x)||\mathrm{Stab}(x)| = |R|$. ↩
3. If you're paying close attention, you'll notice I'm waving my hands over the difference beteween "colorings fixed by $r$" and "rotations that fix $x$". These end up summing to the same thing, and the intuition works either way, but it's an important point. If you want to prove to yourself why they add up to the same thing, imagine drawing a table where the rows are elements of $x$, the columns are rotations in $r$, and each cell has a checkmark depending on if $x$ is fixed by $r$. It should be clear that the order of summation doesn't matter. ↩